Random Variables That Would Be Continuous Example
Continuous Random Variables
In probability theory, a continuous random variable is a number that can take any of an infinite number of values, and whose probability density function is defined over an infinite interval. So, its probability density function cannot be expressed as a simple function of a single real number. Continuous random variables are often regarded as being between 0 and 1, but this is not always the case. For example, the probability density function of a normal distribution is defined over the interval [0, 1], and the probability distribution of a normal random variable is a normal distribution. The continuous random variable can be any of a number of different types. The simplest continuous random variable is the real number, but this variable can take any real values. A continuous random variable can be a real number, a complex number, an integer, a rational number, or an irrational number. A continuous random variable can also be a set of real numbers. (See the article on continuous distribution for additional types of continuous random variables.) Continuous random variables are often characterized by their probability density function (pdf), which is often assumed to be continuous. However, in many cases, the assumption of continuous dependence of the pdf on its arguments is not needed, and often not even true. Further, in many cases, the pdf is not continuous, but follows a power law, in which case the assumption of continuous dependence is an approximation. Continuous random variables are often characterized by their probability distribution, which is often assumed to be a normal distribution. However, in many cases, the assumption of a normal probability distribution is not needed, and often not even true. Further, in many cases, the probability distribution is not normal, but follows a power law, in which case the assumption of a normal probability distribution is an approximation.

Statistics for Business Economics
Draw a graph for the standard normal distribution. Label the horizontal axis at values of $-3,-2,-1,0,1,2,$ and $3 .$ Then use the table of probabilities for the standard normal distribution inside the front cover of the text to compute the following probabilities.
a. $ P(z \leq 1.5)$
b. $ P(z \leq 1)$
c. $ P(1 \leq z \leq 1.5)$
d. $P(0<z<2.5)$


Statistics for Business and Economics
The average amount of precipitation in Dallas, Texas, during the month of April is 3.5 inches (The World Almanac, 2000 ). Assume that a normal distribution applies and that the standard deviation is .8 inches.
a. What percentage of the time does the amount of rainfall in April exceed 5 inches?
b. What percentage of the time is the amount of rainfall in April less than 3 inches?
c. $A$ month is classified as extremely wet if the amount of rainfall is in the upper $10 \%$ for that month. How much precipitation must fall in April for it to be classified as extremely wet?

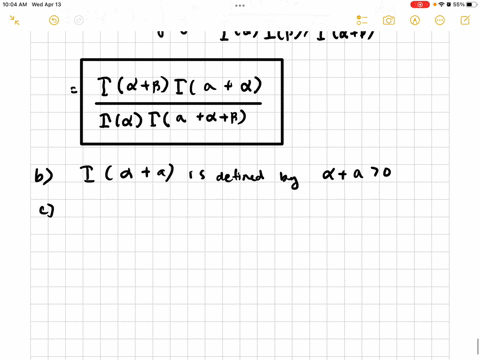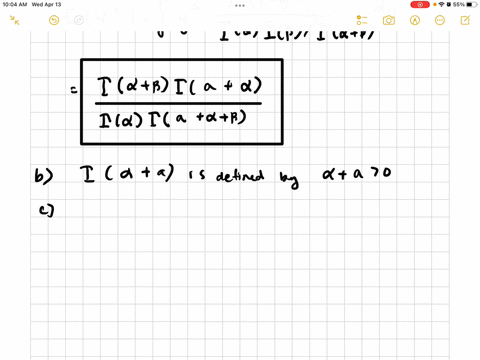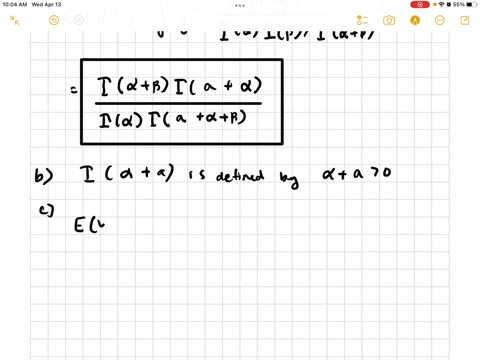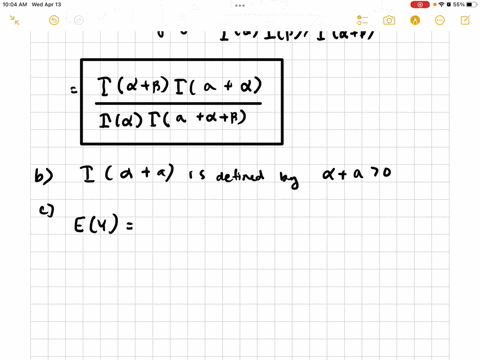
Mathematical Statistics with Applications
Suppose that $Y$ has a beta distribution with parameters $\alpha$ and $\beta$.
a. If $a$ is any positive or negative value such that $\alpha+a>0$, show that
$$
E\left(Y^{a}\right)=\frac{\Gamma(\alpha+a) \Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\alpha+\beta+a)}
$$
b. Why did your answer in part (a) require that $\alpha+a>0$ ?
c. Show that, with $a=1,$ the result in part (a) gives $E(Y)=\alpha /(\alpha+\beta)$
d. Use the result in part (a) to give an expression for $E(\sqrt{Y})$. What do you need to assume about
$\alpha ?$
e. Use the result in part (a) to give an expression for $E(1 / Y), E(1 / \sqrt{Y})$, and $E\left(1 / Y^{2}\right)$. What do you need to assume about $\alpha$ in each case?

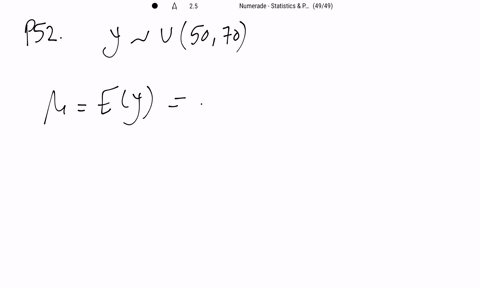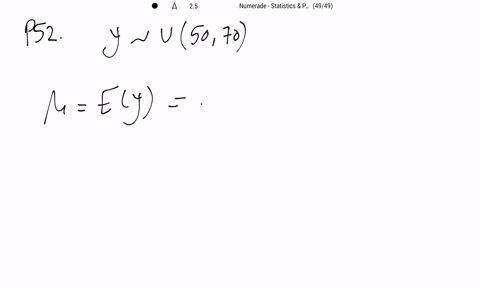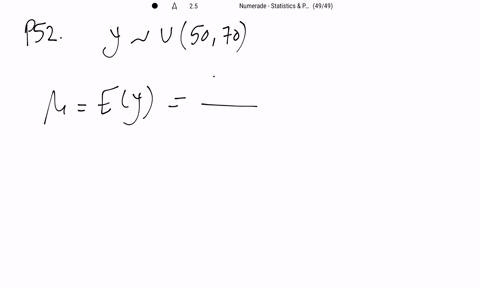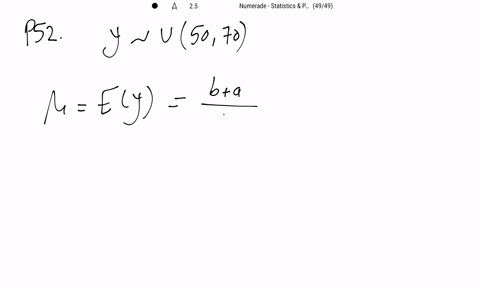
Mathematical Statistics with Applications
Refer to Exercise 4.51 . Find the mean and variance of the cycle times for the trucks.

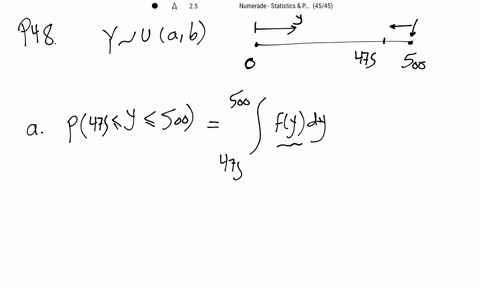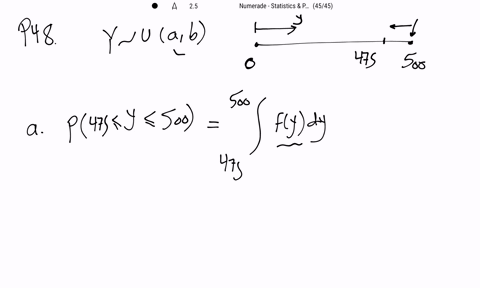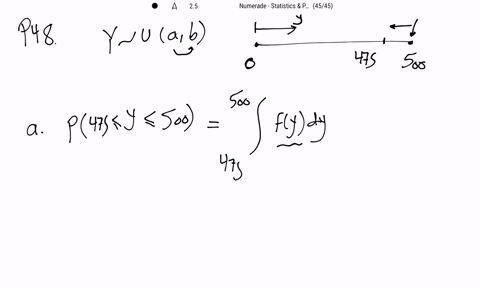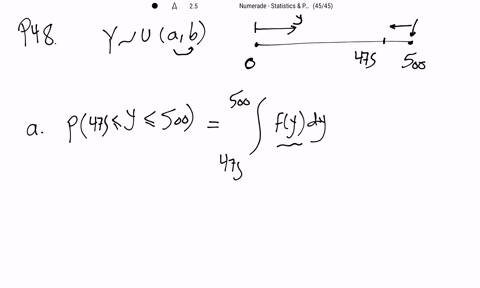
Mathematical Statistics with Applications
If a point is randomly located in an interval $(a, b)$ and if $Y$ denotes the location of the point, then $Y$ is assumed to have a uniform distribution over $(a, b) .$ A plant efficiency expert randomly selects a location along a 500 -foot assembly line from which to observe the work habits of the workers on the line. What is the probability that the point she selects is
a. within 25 feet of the end of the line?
b. within 25 feet of the beginning of the line?
c. closer to the beginning of the line than to the end of the line?

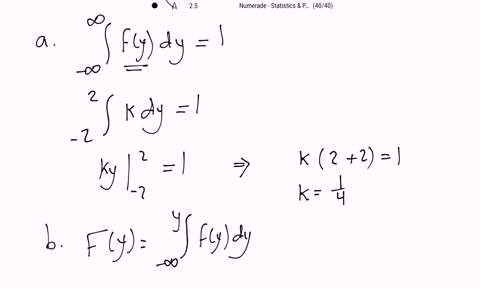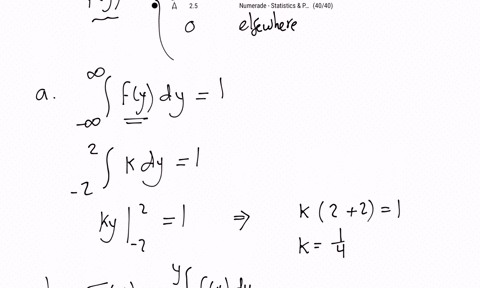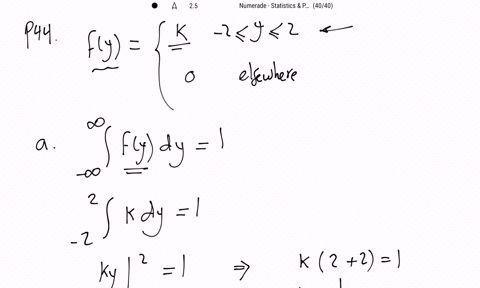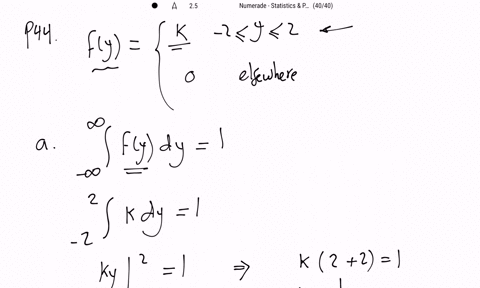
Mathematical Statistics with Applications
The change in depth of a river from one day to the next, measured (in feet) at a specific location, is a random variable $Y$ with the following density function:
$$
f(y)=\left\{\begin{array}{ll}
k, & -2 \leq y \leq 2 \\
0, & \text { elsewhere }
\end{array}\right.
$$
a. Determine the value of $k$.
b. Obtain the distribution function for $Y$.

Introductory Statistics
Let X ~ Exp(0.1).
a. decay rate = ________
b. ? = ________
c. Graph the probability distribution function.
d. On the graph, shade the area corresponding to P(x < 6) and find the probability.
e. Sketch a new graph, shade the area corresponding to P(3 < x < 6) and find the probability.
f. Sketch a new graph, shade the area corresponding to P(x < 7) and find the probability.
g. Sketch a new graph, shade the area corresponding to the 40th percentile and find the value.
h. Find the average value of x.

Introductory Statistics
The time (in years) after reaching age 60 that it takes an individual to retire is approximately exponentially distributed with a mean of about five years. Suppose we randomly pick one retired individual. We are interested in the time after age 60 to retirement.
a. Define the random variable. X = _________________________________.
b. Is X continuous or discrete?
c. X ~ = ________
d. ? = ________
e. ? = ________
f. Draw a graph of the probability distribution. Label the axes.
g. Find the probability that the person retired after age 70.
h. Do more people retire before age 65 or after age 65?
i. In a room of 1,000 people over age 80, how many do you expect will NOT have retired yet?

Introductory Statistics
Use the following information to answer the next 16 exercises. Carbon-14 is a radioactive element with a half-life of about 5,730 years. Carbon-14 is said to decay exponentially. The decay rate is 0.000121. We start with one gram of carbon-14. We are interested in the time (years) it takes to decay carbon-14.
In words, define the random variable $X .$

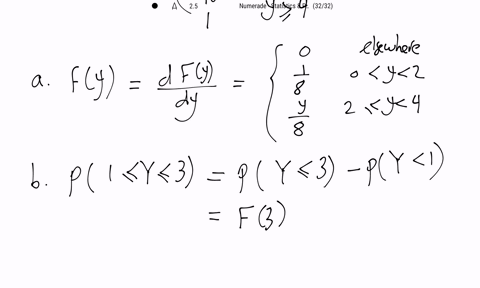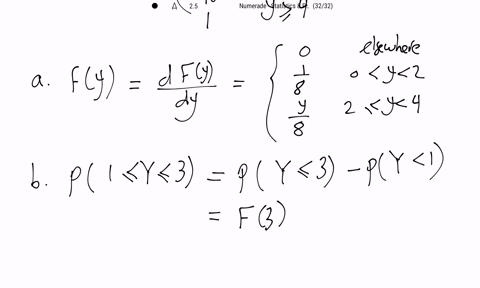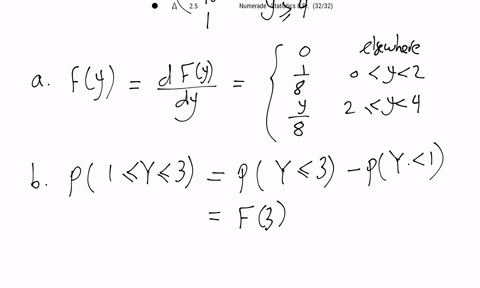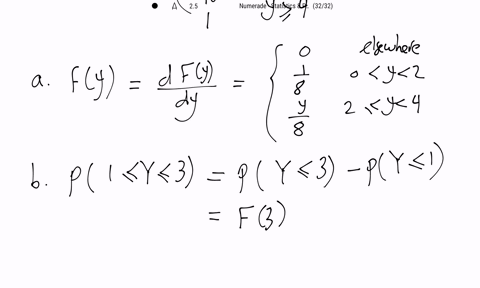
Mathematical Statistics with Applications
Let $Y$ have the density function given by $$f(y)=\left\{\begin{array}{ll}.2, & -1<y \leq 0, \\.2+c y, & 0<y \leq 1, \\0, & \text { elsewhere. }\end{array}\right.$$
a. Find $c$.
b. Find $F(y)$.
c. Graph $f(y)$ and $F(y)$.
d. Use $F(y)$ in part $(b)$ to find $F(-1), F(0),$ and $F(1)$.
e. Find $P(0 \leq Y \leq .5)$.
f. Find $P(Y>.5 | Y>.1)$.

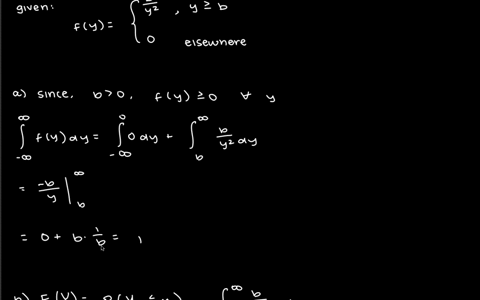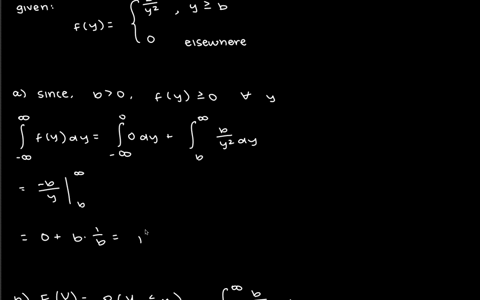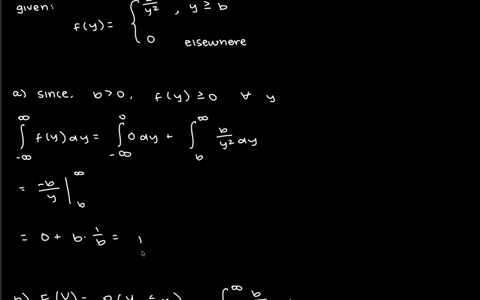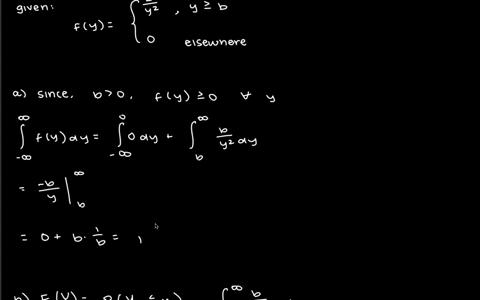
Mathematical Statistics with Applications
As a measure of intelligence, mice are timed when going through a maze to reach a reward of food. The time (in seconds) required for any mouse is a random variable $Y$ with a density function given by $$f(y)=\left\{\begin{array}{ll}\frac{b}{y^{2}}, & y \geq b, \\0, & \text { elsewhere. }\end{array}\right.$$ where $b$ is the minimum possible time needed to traverse the maze.
a. Show that $f(y)$ has the properties of a density function.
b. Find $F(y)$.
c. Find $P(Y>b+c)$ for a positive constant $c$.
d. If $c$ and $d$ are both positive constants such that $d>c,$ find $P(Y>b+d | Y>b+c)$.

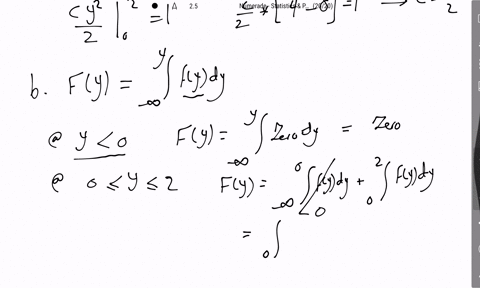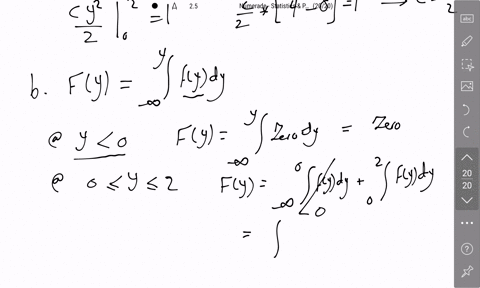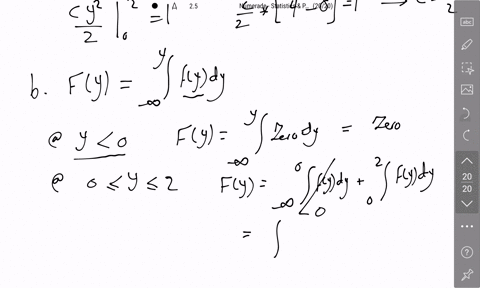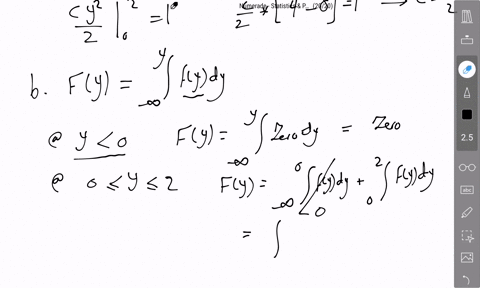
Mathematical Statistics with Applications
Suppose that $Y$ possesses the density function $$f(y)=\left\{\begin{array}{ll}c y, & 0 \leq y \leq 2 ,\\0, & \text { elsewhere .}\end{array}\right.$$
a. Find the value of $c$ that makes $f(y)$ a probability density function.
b. Find $F(y)$.
c. Graph $f(y)$ and $F(y)$.
d. Use $F(y)$ to find $P(1 \leq Y \leq 2)$.
e. Use $f(y)$ and geometry to find $P(1 \leq Y \leq 2)$.

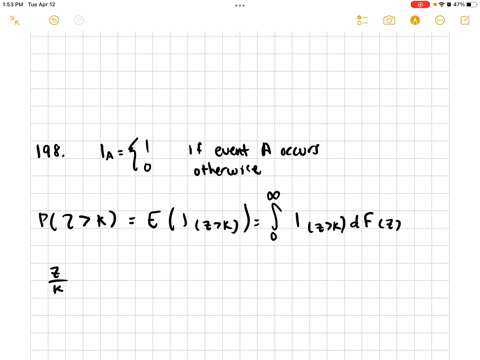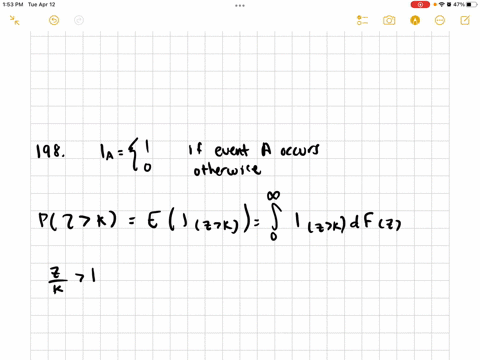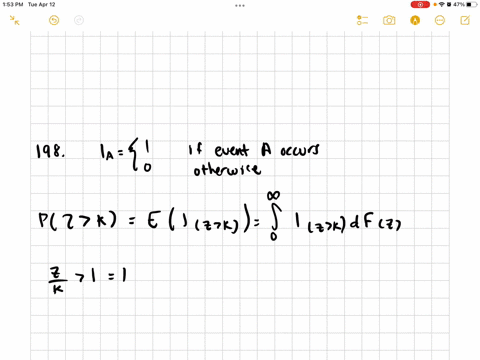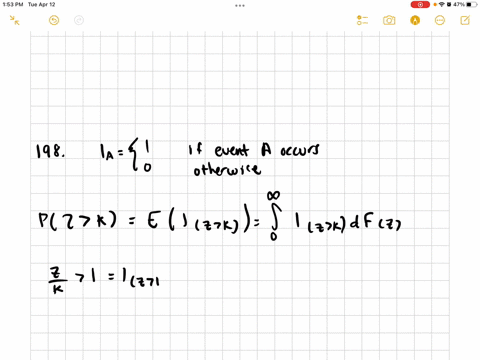
Mathematical Statistics with Applications
The Markov Inequality Let $g(Y)$ be a function of the continuous random variable $Y$, with $E(l g(Y) |)<\infty .$ Show that, for every positive constant $k.$
$$
P(|g(Y)| \leq k) \geq 1-\frac{E(|g(Y)|)}{k}
$$
[Note: This inequality also holds for discrete random variables, with an obvious adaptation in the proof.]

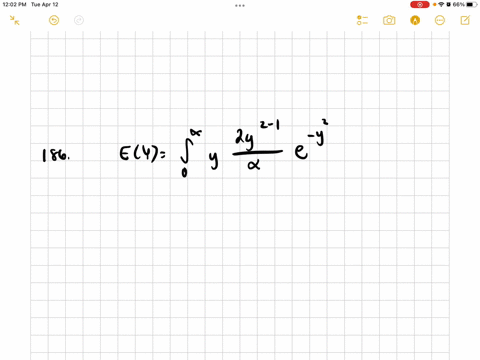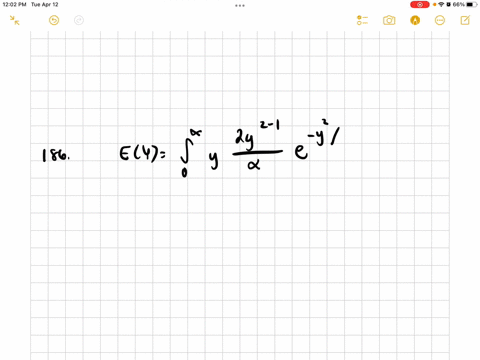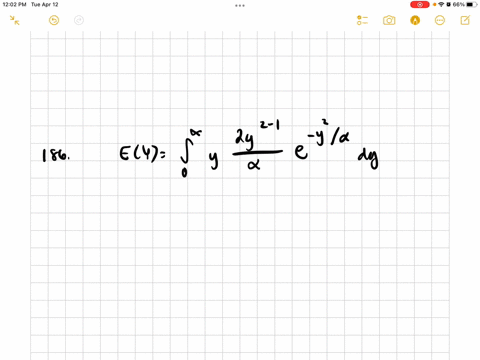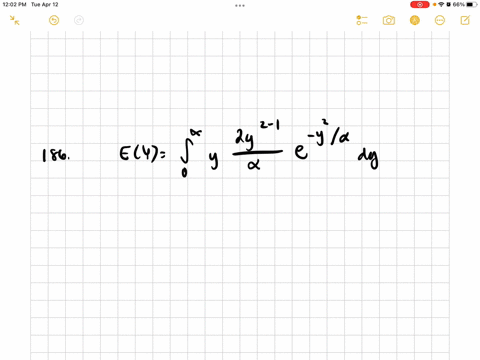
Mathematical Statistics with Applications
The random variable $Y$, with a density function given by
$$
f(y)=\frac{m y^{n-1}}{\alpha} e^{-v / \alpha}, \quad 0 \leq y<\infty, \alpha, m>0
$$
is said to have a Weibull distribution. The Weibull density function provides a good model for the distribution of length of life for many mechanical devices and biological plants and animals. Find the mean and variance for a Weibull distributed random variable with $m=2.$

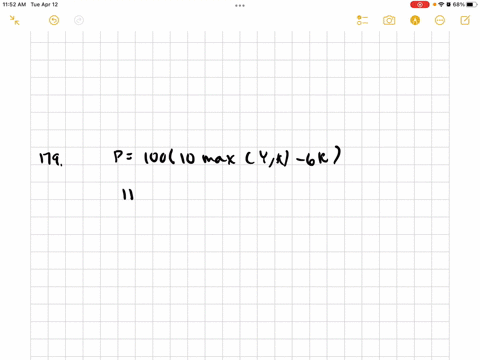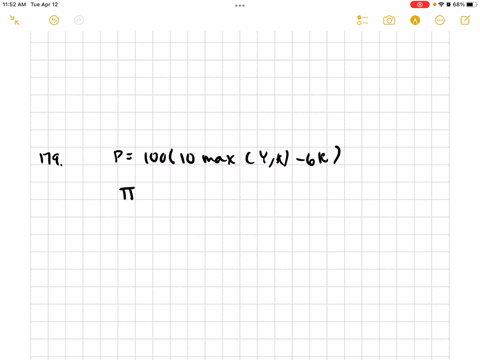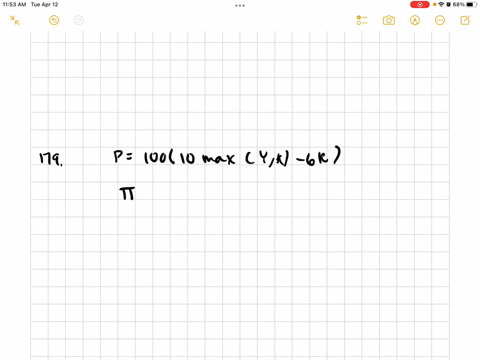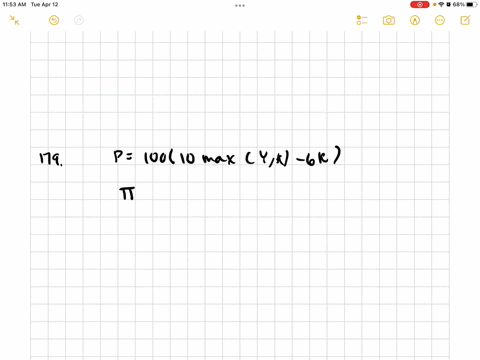
Mathematical Statistics with Applications
A retail grocer has a daily demand $Y$ for a certain food sold by the pound, where $Y$ (measured in hundreds of pounds) has a probability density function given by
$$
f(y)=\left\{\begin{array}{ll}
3 y^{2}, & 0 \leq y \leq 1 \\
0, & \text { elsewhere }
\end{array}\right.
$$
(She cannot stock over 100 pounds.) The grocer wants to order $100 k$ pounds of food. She buys the food at $6 \mathrm{c}$ per pound and sells it at $10 \mathrm{c}$ per pound. What value of $k$ will maximize her expected daily profit?

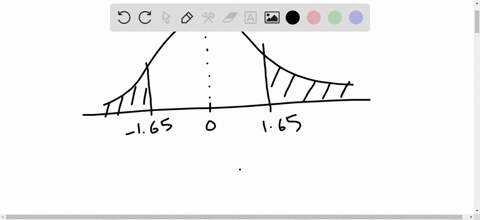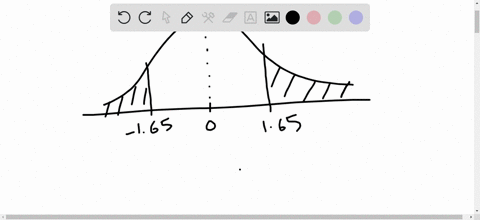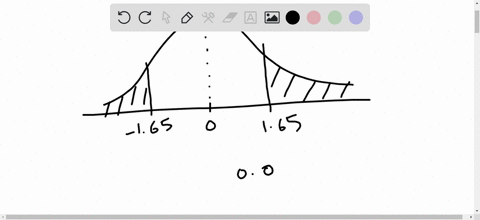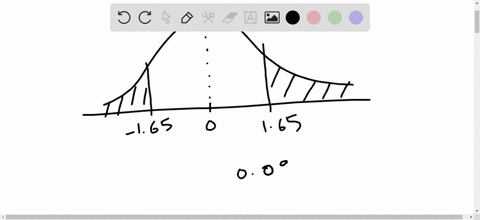
Elementary Statistics: Picturing the World
Find the indicated probability using the standard normal distribution. If convenient, use technology to find the probability.
$P(-1.65<z<1.65)$

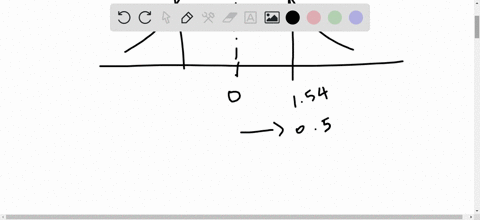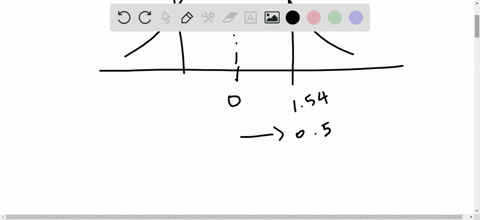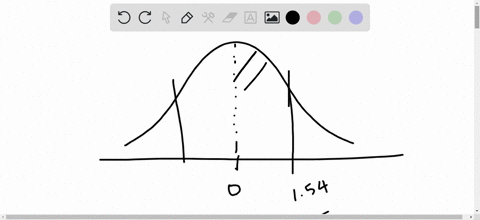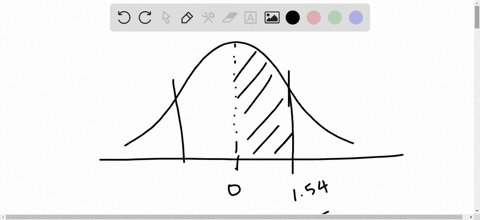
Elementary Statistics: Picturing the World
Find the probability of $z$ occurring in the indicated region of the standard normal distribution. If convenient, use technology to find the probability.
(FIGURE CAN'T COPY)

Elementary Statistics: Picturing the World
Find the probability of $z$ occurring in the indicated region of the standard normal distribution. If convenient, use technology to find the probability.
(FIGURE CAN'T COPY)

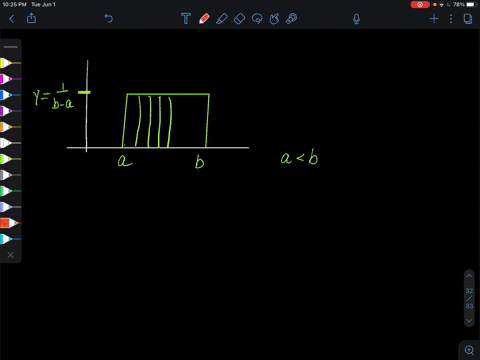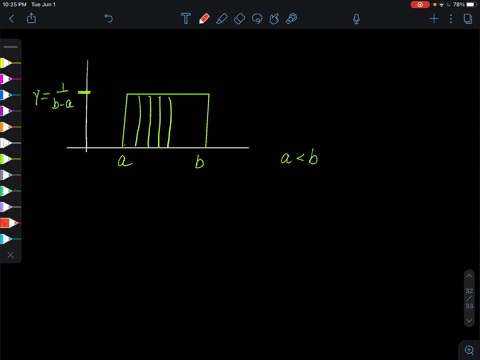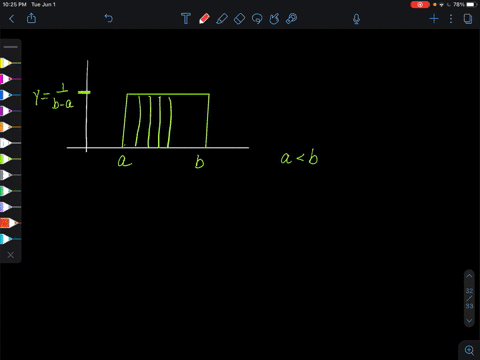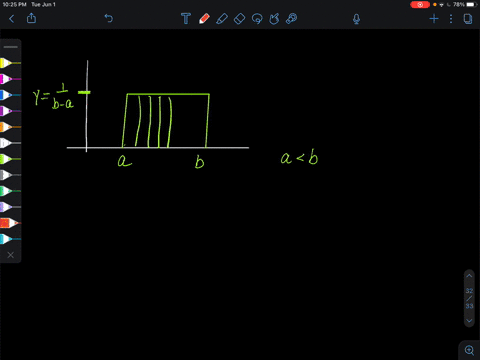
Elementary Statistics: Picturing the World
A uniform distribution is a continuous probability distribution for a random variable $x$ between two values a and $b(a<b),$ where $a \leq x \leq b$ and all of the values of $x$ are equally likely to occur. The graph of $a$ uniform distribution is shown below. (FIGURE CAN'T COPY) The probability density function of a uniform distribution is
$$y=\frac{1}{b-a}$$ on the interval from $x=a$ to $x=b .$ For any value of $x$ less than a or greater than $b, y=0 .Use this information.
Show that the probability density function of a uniform distribution satisfies the two conditions for a probability density function.

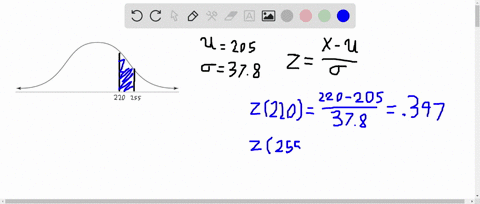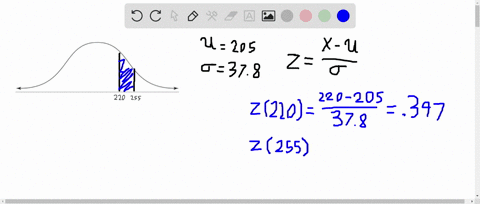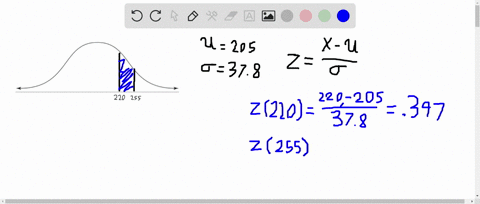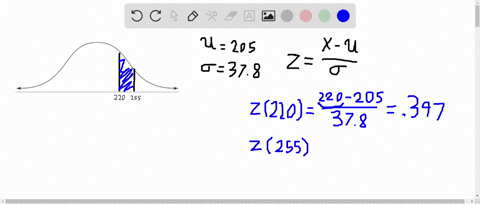
Elementary Statistics: Picturing the World
A member is selected at random from the population represented by the graph. Find the probability that the member selected at random is from the shaded area of the graph. Assume the variable $x$ is normally distributed.
(Check your book to see graph)

Elementary Statistics: Picturing the World
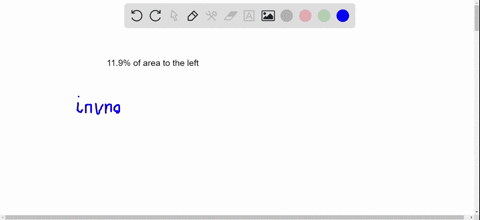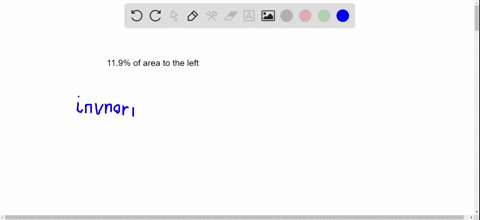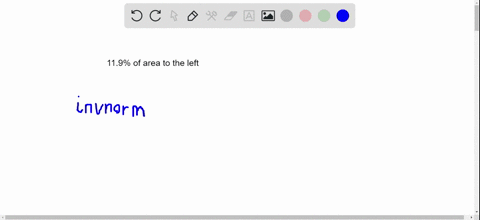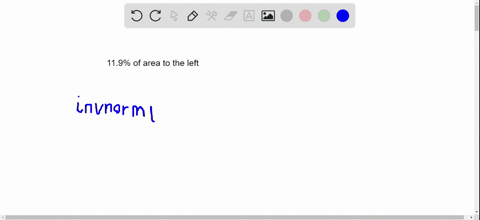
Find the indicated z-score.
Find the $z$ -score that has $11.9 \%$ of the distribution's area to its left.

Source: https://www.numerade.com/topics/continuous-random-variables/
0 Response to "Random Variables That Would Be Continuous Example"
Post a Comment